大道至简:朴素贝叶斯分类器
万物之始,大道至简,衍化至繁。
——ifelse(is.element(this, 道德经), 道德经, unknown)
一、背景
提到贝叶斯分类,首先来看下贝叶斯其人,贝叶斯(Thomas Bayes,1701—1761)英国牧师、业余数学家。可别小看了欧洲的牧师,孟德尔,被誉为“遗传学之父”也曾为一名神父,假如你不记得孟德尔是谁,那么你肯定记得高中生物上那个著名的豌豆实验。
具有讽刺意味的是,当初贝叶斯发明概率统计理论是为了证明上帝的存在,而至死这个愿望都没有实现,不过感谢伟大的贝叶斯,因为他的无心插柳,才有了今天的贝叶斯公式。接下来,来一睹贝叶斯公式的风采,
$$P(B|A)=\frac{P(B)P(A|B)}{P(A)}$$
公式看起来是不是很简洁,看起来很有对称美。记得上学那会数学老师的一句话,假如你算出来的答案不够简洁,那么多半这道题你算错了。贝叶斯公式有什么意义呢?它解决了两个事件条件概率的转换问题。比如说,已知感冒导致流鼻涕的概率,那么流鼻涕有多大的概率感冒呢?贝叶斯可以解决这类问题。
二、贝叶斯分类
贝叶斯可以解决条件概率转换,可是它怎么与分类联系起来的呢?
让我以一个例子加以说明,假设有这样一个数据集(本例来自朴素贝叶斯分类器的应用),
症状(A1) 职业(A2) 疾病(B)
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡
那么一个打喷嚏的建筑工人是感冒还是没感冒呢?
根据贝叶斯定理,
P(感冒|打喷嚏x建筑工人) = P(打喷嚏x建筑工人|感冒) x P(感冒) / P(打喷嚏x建筑工人)
假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人) = P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) / P(打喷嚏) x P(建筑工人) = 0.66 x 0.33 x 0.5 / 0.5 x 0.33 = 0.66
同理,
P(非感冒|打喷嚏x建筑工人) = P(打喷嚏|非感冒) x P(建筑工人|非感冒) x P(非感冒) / P(打喷嚏) x P(建筑工人) = 0.33 x 0.33 x 0.5 / 0.5 x 0.33 = 0.33因为P(感冒|打喷嚏x建筑工人) > P(非感冒|打喷嚏x建筑工人) ,所以我们更愿意相信一个打喷嚏的建筑工人是感冒的。
从上面的例子可以看出,贝叶斯分类的步骤是这样的:
- 设$x = {a_1,a_2,\cdots}$为一个待分类项,每个a为x的一个特征属性。
- 有类别集合$C = {y_1,y_2,\cdots,y_n}$.
- 根据训练集计算,$P(y_1|x), P(y_2|x),\cdots,P(y_n|x)$.
- 如果$P(y_k|x)=max{P(y_1|x), P(y_2|x),\cdots,P(y_n|x)}$,则$x$的分类为$y_k$。
说到贝叶斯分类,还有几个需要注意的问题:
- 如果已知条件不止一个属性,二是多个呢,这个时候贝叶斯公式可以写作$$P(y|a_1a_2\cdots)=\frac{P(y)P(a_1a_2\cdots|y)}{P(a_1a_2\cdots)}=\frac{P(y)P(a_1|y)P(a_2|y)\cdots}{P(a_1)P(a_2)\cdots}$$上述公式假设特征属性$a_1,a_2\cdots$相互独立,这也是“朴素”一词的由来。另外,可以看到对于不同的分类,分母都是恒定的,而我们只想找到概率最大的类别,因此可以把分母省略,求条件概率的相对值,$$P(y|a_1a_2\cdots)_{relative}=P(y)P(a_1|y)P(a_2|y)\cdots$$
- 不知道大家有没有注意到,上面的已知条件都是离散值,如果是连续值呢,对于连续值通常有两种办法,一是将连续值截取为离散值,然后求概率,二是假定离散值服从高斯分布,即$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})$$因为我们只需求概率的相对值,所以这里只需计算属性的概率密度值即可。
- 还有一个问题,当某些类别下某个特征值计数为0,即$P(a_i|y_j)$=0,这会使某些分类最终的概率为0,会降低分类器的准确性,为了解决这个问题,引入Laplace校准,就是对这些类别的某些特征值计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响。
如果想更详细的了解贝叶斯分类,请参考这两篇文章分类算法之朴素贝叶斯分类和朴素贝叶斯分类器的应用。
接下来,我用R语言实现一个分类器并用一些数据集测试分类效果。
三、算法实现
程序主要由三部分组成:
分类器主要由下面几个函数组成,具体的代码见GitHub。
# 1.求各个分类概率P(ycol)
get.ytable <- function(ycol, trainset)
# 2.1求离散属性xcol的条件概率P(xcol|ycol)
get.discrete.xtable <- function(xcol, ycol, trainset)
# 2.2求连续属性xcol的概率密度,假设服从高斯分布
get.continout.xdensity <- function(xcol, ycol, trainset)
# 3.对于某些概率为零的类别,采用Laplace校准设置默认值
get.defaultx <- function(ycol, trainset)
# 注:xcol特征属性,ycol类别属性,trainset训练集
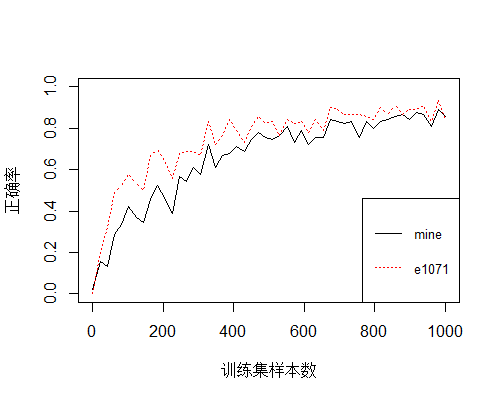
下面以基础包里的iris数据集验证一下分类器的效果,选取前四列为特征,预测鸢尾花的种类,
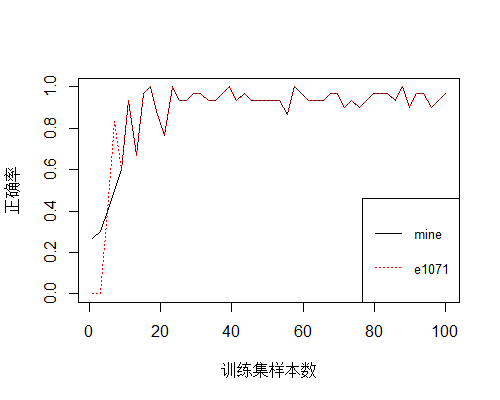
图上有两条曲线,黑色为我实现的贝叶斯分类器,红色虚线为e1071包里的一个贝叶斯分类器实现。观察可得,随着训练集样本数的增加,测试集的分类正确率越来越高。
再来看看特征属性的选取对正确率的影响,
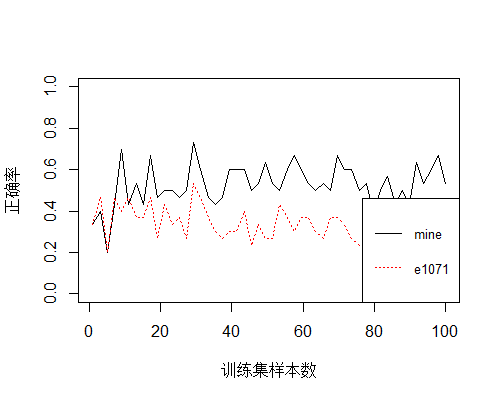
这次只选择了第二列(花萼宽度)作为特征值,可以看到正确率明显下降了。
再来看一个多分类问题,采用北京二手房这个数据集,
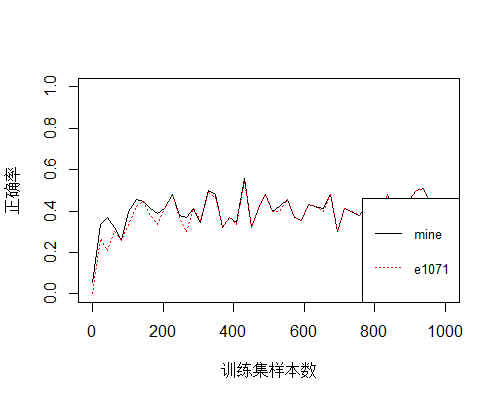
通过房价和是否学区这两列来预测房子所在的区,可以看到这两个特征属性的预测正确率稳定在0.4左右,下面再添加户型、朝向、楼层三列,
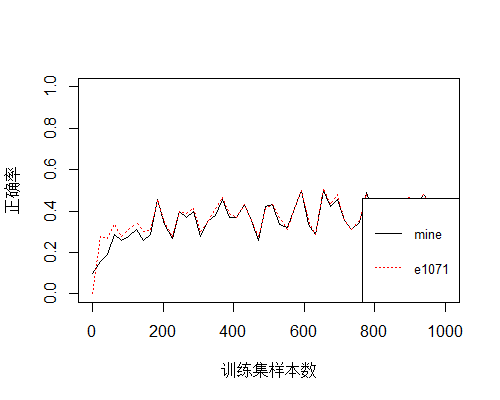
上图显示,添加了三个特征属性后,正确率并没有明显的改善,但是如果再添加一个区域列(con),
由图观察,添加了区域这一列后,正确率得到了大幅度的提升,事实上仅保留区域这一列,预测的正确率也很高,这是因为区域(con)与区(area)的相关性较强。
根据我实验的结果,通常情况下,提高预测正确率的方法有两种:
- 增加训练集样本数,但是样本到达一定的数目正确率就保持稳定,很难再提高了。
- 选取恰当的特征,注意单纯的增加特征数目并不能提高正确率,反而会引入更多的误差造成过拟合。