简洁高效的Boyer-Moore算法
子串检索有着很广泛的应用,例如在文档软件中查找关键词,网站过滤敏感词,生物学家查找某种模式的基因组序列等等,很多人听说过著名的KMP算法,Boyer-Moore算法做到的更多,有迹象表明在某些情况下效率是前者的3-5倍,且实现起来更加简单,符合我简单高效的原则。
下面先抛开算法不谈,如果让你在ABCSAKDFFEHHJDDEFKLD中查找DDEFK,你会怎么做?
ABCSAKDFFEHHJDDEFKLD
DDEFK
最直接的就是暴力检索法,挨个比较文本和模式的每个字符,成功就继续比较模式字符的下一个,否则将模式往右移动一位,继续上述过程,直到文本的结尾或者搜索成功,通常情况下效率还可以,因为对于大部分文档往往只需要比较模式中的一两个字符,就会有非匹配字符,因此模式可以快速的向右移动,整体运行时间接近线性。java示例代码为
int M = pat.length();
int N = txt.length();
for(int i = 0; i <= N - M; i++) {
for (int j = 0; j < M; j++) {
if (txt.charAt(i + j) != pat.charAt(j)) {
break;
}
if (j == M - 1) {
return i;
}
}
}
return -1;
而本文的主角BM算法可谓别出心裁,它从后往前匹配模式的每一个字符,看看BM算法是如何处理上面的例子的,我们用i表示文本的起始位置,j表示模式中待匹配字符的位置。
第一步,i=0,j=4,A与K匹配失败,没有必要再往前匹配,i往后移动4+1=5个字符,因为小于这个数字,A都会与模式中的某个字符重叠,而模式中没有这个字符,无论如何都会失败。
i=0
ABCSAKDFFEFKJDDEFKLD
DDEFK
j=4
第二步,i=5,j=4,E与K匹配失败,i需要再次往后移动,这次需要移动几个字符呢,答案是2,这样会将模式中最右边的E与文本中E对齐,小于这个数,文本中E会与模式E右边的字符重叠,这些字符中没有E,因此不可能成功。
i=5
ABCSAKDFFEFKJDDEFKLD
DDEFK
j=4
第三步,i=7,j=4,这次匹配成功了,j减一j=3,又成功了,j再减一j=2,又成功了,j再减一j=1,这次F与D没有匹配成功,这次i要移动多少呢,F在文本和模式中都出现了,但是模式中的F已经匹配过了,我们不想让i回退,只能让i简单的加1。
i=7
ABCSAKDFFEFKJDDEFKLD
DDEFK
j=4
j=3
j=2
j=1
第四步,i=8,j=4,同样J和K匹配失败,且J不在模式字符串中,同第一步,我们将i移动4+1=5个字符。
i=8
ABCSAKDFFEFKJDDEFKLD
DDEFK
j=4
第五步,i=13,k=4,当j=4…0时,每个字符都匹配成功,成功检索到模式,将i=13返回,或者将i的值存储起来继续往后搜索,如果想得到模式的所有位置。
i=13
ABCSAKDFFEFKJDDEFKLD
DDEFK
j=4
j=3
j=2
j=1
j=0
这样i移动5次,总共比较了12个字符,就完成了查找。
总结一下,BM算法的策略是从后往前匹配模式中的每个字符,直到文本中出现一个不匹配的字符txt.charAt(i+j)或者检索成功返回i。与暴力检索不同的是,当匹配失败时,BM算法不会按部就班的移动i,它首先会构造一个right数组,数组中存储的是字符集中每个字符在模式中最右边的位置,如果字符不在模式中设为-1,比如上面的例子,
right['D']=1
right['E']=2
right['F']=3
right['K']=4
下面是可能出现的三种情形,
-
当非匹配字符
txt.charAt(i+j)不在模式中时,就像上面第一步那样,i需要右移j+1个字符,否则非匹配字符就会与模式字符串的某个字符重叠。 -
当非匹配字符
txt.charAt(i+j)是模式中一员时,如上第二步那样,i需要右移j-right[txt.charAt(i+j)],小于这个步数也会发生重叠。 -
第三种情形其实是第二种情形的补充,虽然非匹配字符
txt.charAt(i+j)在模式中,但是已经比较过,这样j-right[txt.charAt(i+j)] < 1,这种情形下只让i简单的右移1位。
这是一段示例代码,
public List<Integer> search(String txt) {
int N = txt.length();
int M = pat.length();
List<Integer> pos = new ArrayList<>();
for (int i = 0, skip = 0; i <= N - M; i += skip) {
for (int j = M - 1; j >= 0; j--) {
if (pat.charAt(j) != txt.charAt(i + j)) {
skip = j - right[txt.charAt(i + j)];
if (skip < 1) {skip = 1;}
break;
}
if (j == 0) {
pos.add(i);
skip = M;
break;
}
}
}
return pos;
}
上面的代码会找出文本中模式出现的所有位置,在大部分情况下,上面这段代码的运行效率为$O(N/M)$,但是,当文本中包括大量的重复字符时,搜索的效率为$O(NM)$,请看下面的例子,
txt length: 20
pat length: 5
--------------------
BBBBBBBBBBBBBBBBBBBB
ABBBB #0 0
ABBBB #1 5
ABBBB #2 10
ABBBB #3 15
ABBBB #4 20
ABBBB #5 25
ABBBB #6 30
ABBBB #7 35
ABBBB #8 40
ABBBB #9 45
ABBBB #10 50
ABBBB #11 55
ABBBB #12 60
ABBBB #13 65
ABBBB #14 70
ABBBB #15 75
每一步后面有两个数字,第一个数字表示i移动的次数,后一个表示比较的字符数,如上所示,这个例子i移动了15次,总共比较了75个字符,接近于20*5,效率为$O(NM)$。这不是我们想看到的,为了应对这种情形需要引进另一个数组delta,delta数组中存储的是文本中每个字符最后出现的地方,默认值为模式的长度,这样当遇到非匹配字符txt.charAt(j)时至少delta[pat.charAt(j)]-j这一段是不可能匹配的,因为在文本中这一段没有出现pat.charAt(j),比较的时候就有了两个移动距离,取其大者。下面是新的代码,
public List<Integer> search(String txt) {
int N = txt.length();
int M = pat.length();
List<Integer> pos = new ArrayList<>();
for (int i = 0, skip = 0; i <= N - M; i += skip) {
for (int j = M - 1; j >= 0; j--) {
char c1 = txt.charAt(i + j);
char c2 = pat.charAt(j);
delta[c1] = j;
if (c1 != c2) {
int skip1 = j - right[c1];
int skip2 = delta[c2] - j;
skip = Math.max(skip1, skip2);
if (skip < 1) {skip = 1;}
break;
}
if (j == 0) {
pos.add(i);
skip = M;
resetDelta();
break;
}
}
}
return pos;
}
每次匹配成功,需要重置delta数组,即上面resetDelta()。将这段代码与上面那一版进行对比,看看有哪些区别。完整代码在这里,用这一段代码再运行上面的例子,
txt length: 20
pat length: 5
--------------------
BBBBBBBBBBBBBBBBBBBB
ABBBB #0 0
ABBBB #1 5
ABBBB #2 10
ABBBB #3 15
这次好多了,i移动了3次,只比较了15个字符,就完成了整个检索,算法复杂度基本为线性。好了,算法分析与证明不是那么有意思,最后就以我做的两个实验来结束吧。
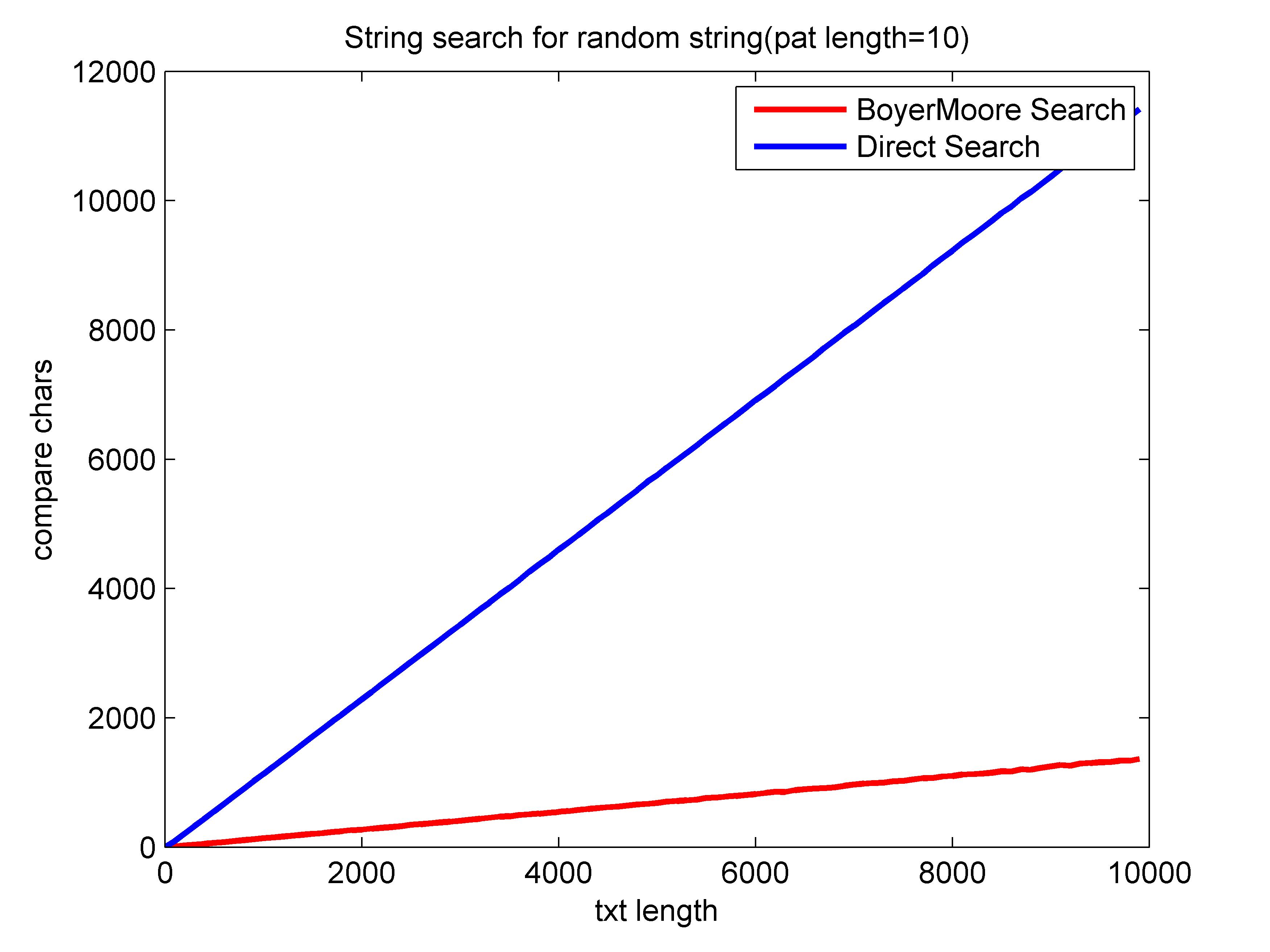
横轴为文本长度,纵轴表示比较的字符数,文本和模式从26个大写字母随机生成。可以看到,对于长度为10的模式,BM算法复杂度大约为$O(N/M)$,暴力检索为$O(N)$。
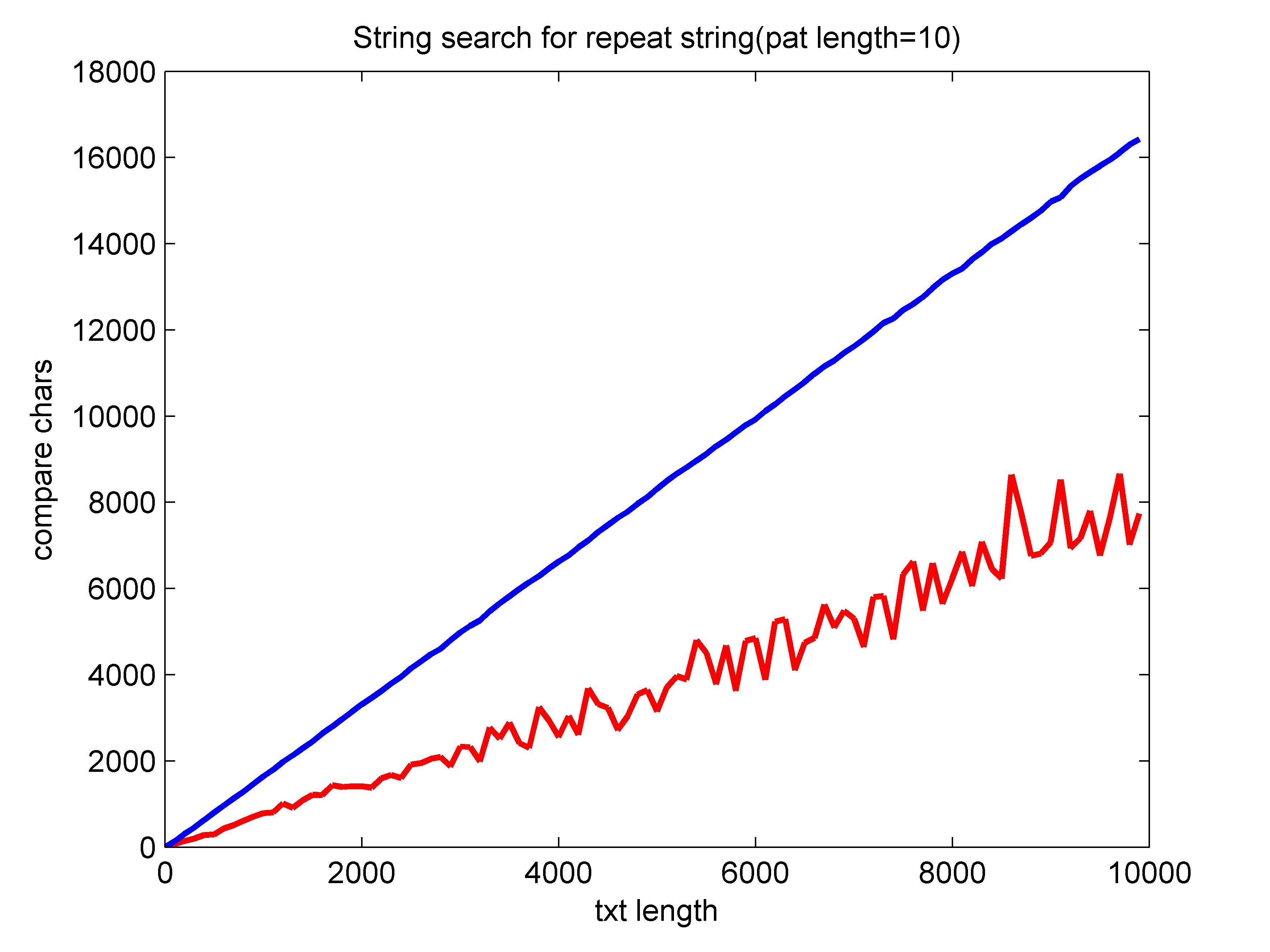
与上图不同,这幅图的文本和模式是从4个大写字母随机选择,因此重复率要高的多。可以看到,对于重复率很高的字符串,BM算法效率也能达到$O(N)$,而暴力检索接近$O(NM)$。