加密和解密
最近学习HTTPS的知识,涉及了一些加密和解密的内容,在Mozilla MDN上找到一篇文章*Encryption and Decryption*,清晰明了,特地翻译一下,与大家分享。
**加密(Encryption )**是将原始信息转化为对其他用户非明了信息的过程,除非信息的接受者;解密(Decryption)是将非明了信息转化为原始数据的过程。加密算法,也称作密码(cipher, 注:与传统意义上的密码不同),是一种用来加密和解密的数学函数。在大多数情况下,会同时采用两个相关的函数,一个用作加密,另一个用作解密。
当今的大多数加密技术保持信息私密并不依靠算法本身,因为算法都是众所周知的,而是依靠加密和解密的密钥(key)。使用正确的密钥进行解密轻而易举,而使用不正确的密钥想进行解密是非常困难的,在某些实际情况下,可以说是不可能的。
本篇文章将从下面三个方面介绍密钥在加密和解密中的用处:
- 对称密钥加密(Symmetric-Key Encryption)
- 公钥加密(Public-Key Encryption,也称作非对称密钥加密)
- 密钥长度和加密强度
对称密钥加密
在对称密钥加密中,加密密钥可以由解密密钥推知,反之亦然。事实上,在很多情况下,二者是相同的,如下图所示。
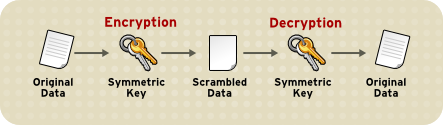
对称密钥加密效率非常高,以至于用户几乎察觉不到加密和解密的延迟。对称密钥加密还提供了一定程度的认证机制,因为信息一旦经密钥加密,不可能被其他密钥解密。因此,只要密钥没有泄露且信息可以正确的解密,通信双方都能确定是在与对方通信。
只有在通信双方保持密钥不被泄露的情况下,对称密钥加密才是有效的。如果其他人发现了密钥,将会影响双方的私密性和身份认证。一个未经授权的用户不仅可以使用密钥解密消息,还可以加密和发送一条新消息给通信中的一方,就好像它是拥有此密钥的另一方一样。
对称密钥加密在SSL协议中扮演着重要的角色,它广泛地应用在身份认证、篡改监测以及 TCP/IP网络加密中。另外,SSL也使用了公钥加密,下一节将介绍这种技术。
公钥加密
公钥加密最常用的实现是基于RSA Data Security的专利算法,因此,本节将以RSA这种方式介绍公钥加密。
公钥加密包括一对密钥:一个公钥和一个私钥——还有对其进行电子认证、签名和数据加密的实体。公钥是公开的,而对应的私钥是保密的。公钥加密的数据只能被对应的私钥解密。下图简单展示了公钥加密的工作方式。
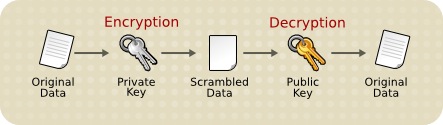
上图这种方案可以让你自由发布一个公钥,只有你才能使用公钥读取加密的数据。一般情况下,为了给某些人发送加密数据,你首先使用那人的公钥进行加密,那人收到加密数据后使用对应的私钥进行解密。
对比对称密钥加密,公钥加密需要更大的计算量,因此当数据量比较大时,这种加密方式就不太合适了。然而,可以使用它发送一个对称密钥,然后再用这个对称密钥加密另外的数据(注:这里有两个过程,第一步公钥加密,第二步对称密钥加密)。SSL正是使用的这种方式。
就像上图显示的那样,上面的方案反过来同样适用(注:我觉得原文说反了,图中展示的就是这种方案):使用私钥加密,然后使用对应的公钥解密。对于敏感数据,这不是一个理想的方式,因为根据定义,拥有公钥的任何人都可进行解密。尽管如此,使用私钥进行加密这种方式还是非常有用的,因为这意味着你能够使用你的私钥进行电子签名,这在电子商务及其他商业应用程序加密中非常重要。客户端程序比如Firefox能够使用你的公钥来确认这份使用你的私钥加密的消息是否被篡改。*数字证书是什么*这篇文章介绍了这个确认过程。
密钥长度和加密强度
破解一个加密算法就是要找到将加密数据变为原始数据的密钥。对于对称密钥加密来说就是要找到进行数据加密的密钥,对于公钥加密来说,就是获得通信双方的私钥。
破解对称密钥加密的一个方式是挨个测试算法中的每个密钥直到找到正确的密钥。对于公钥加密,密钥对中的一个(公钥)是公开的,另一个(私钥)经过已经公布的复杂数学计算得到。挨个测试密钥的方法被称作暴力破解法。
加密算法被破解将会带来私密信息被拦截、被冒充甚至被欺诈的风险。
加密算法的密钥强度是由破解此算法的最快方法与暴力破解法的速度对比值确定(注:意思是最快的破解方法和暴力破解速度差不多那么密钥强度高,如果最快的破解方法比暴力破解快得多那么密钥强度低)。
对于对称密钥,加密的强度是由加密密钥的长度或者大小确定的:一般情况下,密钥越长,强度越高。密钥长度是使用位(bit)进行衡量的。例如,SSL协议的RC4对称密钥加密算法,128位的密钥要比40位的密钥安全的多。大致来说,128位的RC4加密强度是40位的RC4加密强度的3 x 1026倍(关于SSL中RC4加密的更多信息,详见*Introduction to SSL*)。如果加密密钥已知最快的破解方法和暴力破解差不多,那么就可以说这个密钥是强力的(full strength)。
不同的加密算法可能需要不同的密钥长度来达到同样的加密强度。例如,公钥加密中的RSA算法,因为它所基于数学原理,密钥只能是给定长度所有值的一个子集。其他加密算法,比如对称密钥加密的用到的算法,密钥可以是给定长度所有值,而不只是一个子集。
因为RSA密钥破解起来相对容易,RSA加密算法的密钥长度要比较长,为了达到较高的加密强度,至少要达到1024位。相比之下,对于对称密钥加密的大部分算法,达到同样的加密强度,密钥长度只需要80位。