疏而不漏:随机森林
一、概述
在三生万物:决策树中我们提到当决策树和装袋法(Bagging)和提升法(Boosting)结合后会成为更强大的算法,那么今天就介绍一种名叫随机森林(Random Forest)的算法,它是将决策树、装袋法以及随机特征选取结合后衍生出的一种增强型的树算法。
它有如下特点:
- 运行起来非常有效率,可以很容易的并行化
- 可以无删减的处理成千上万的输入变量,并可以评估变量的重要性
- 不用将数据专门分为训练集和测试集,随机森林构造完就可以得到近似的测试误差
- 能够很有效的处理缺失值
- 可以有效的分离出离群点
- 对过拟合有很强的抗性
- 还可以用于非监督式学习
……
看到随机森林有这么多的优点,你是不是心动了呢?那么接下来和我一起来认识一下它吧!
二、算法
1、基本步骤
上文提到随机森林不是一种全新的算法,而是几种算法的强强联合。随机森林的构建一般有这么几个步骤:
- 首先确定树的数量(Tree Size),而每个树的训练数据通过有放回的抽取原始数据。由于是有放回的抽样,原始数据中约有1/3的量没有被抽到,这些数据称为袋外数据(OOB, Out Of Bag)
- 树的树训练数据有了,接下来就该训练了,与决策树不同,这里的树在构建的时候,每一次分裂都要进行随机特征选取,也就是在特征的随机子空间进行分裂,比如一个数据集有5个特征,每次分裂有放回的随机取3(Feature Count)个
- 到这里,所有的树都应该构造完成了,森林也就有了,那么怎么对响应值进行预测呢?这就要依靠集体的智慧了,每个树都有一个预测值,对于分类问题,取频率最高的那个值;对于回归问题,取所有值的平均
2、袋外误差(OOB Error)
算法作者说OOB Error可以作为测试误差的无偏估计,也就是计算出OOB Error就可以得到测试误差,不用专门把数据专门拿出来一部分作为测试集。下面举例说明如何计算OOB Error,比如我们要在一个有7条数据的数据集上构建一个5棵树的随机森林,那么在步骤1的时候会出现下面这样一张表:
| 数据编号 | 树1 | 树2 | 树3 | 树4 | 树5 |
|---|---|---|---|---|---|
| 1 | X | √ | √ | X | √ |
| 2 | √ | X | X | X | X |
| 3 | √ | √ | √ | √ | √ |
| 4 | √ | √ | X | √ | √ |
| 5 | √ | X | √ | √ | X |
| 6 | √ | √ | X | √ | √ |
| 7 | X | √ | √ | √ | √ |
表里的X代表没有选中,√代表选中。对于树1,数据1和7就是OOB,对于树2,数据2和5就是OOB,其他以此类推,那么数据1的预测值由树1和树4决定,数据2的预测值由树2-5来决定,以这样的方式计算出每个数据的预测值,进而得到误差值,即OOB Error。
3、变量重要性(Variable Importance)
假设我们已经计算出了OOB Error,一个变量的重要性可以这么计算,将变量打散,然后重新计算打散后的OOB Error,取打散前后OOB Error差值的绝对值,越大代表这个变量越重要。变量重要性在实践过程中非常好用,比如在一个10000维度的数据集选出100个最重要的变量,即数据的降维。
4、相似性(Proximities)
相似性由相似性矩阵体现,相似性矩阵是一个NxN的对称矩阵,它的计算方式如下,如果数据n和数据p同属于同一颗树的同一个叶子节点,那么相似性加1,即proximities[n,p]和proximities[p,n]均加1,最后除以树的数目进行标准化。
5、离群点(Outliers)
有了相似性,也就可以计算离群点了。它基于这样的假设,如果一条数据和其他数据都不相似或者相似性很低,那么这条数据很可能是个离群点。这和人很类似阿,如果一个人不合群,那么他肯定是比较孤立的。不过在我实际操作的过程中,即使计算出了潜在的离群点,如何确定它真的是不是不是那么容易。
具体的计算过程如下,定义类别为j的数据n的平均相似性为:
$$\bar{P}(n) = \sum_{cl(k)=j}prox^2(n,k)$$
得到非相似性:
$$Dissimilarity(n) = nsample(j) / \bar{P}(n)$$
然后在各自的类别中标准化,得到最终的Dissimilarity,算法作者给出的经验值是如果一条数据的Dissimilarity>10,那么可能是一个潜在的离群点。
6、缺失值
对于缺失值,传统的方法就是数值变量取均值,分组变量取最多的那一类。而随机森林处理缺失值另有一套:先使用一个不太准确的初始值替换缺失值,然后计算数据间的相似性,数值变量取同一类别非缺失值的相似性加权平均;分组变量取频率最高的值,频率要经过相似性加权,然后重复这一过程4-6次。
三、案例
在决策树代码的基础上稍加改动就得到了随机森林,下面检验一下新算法的能力。
1、在三生万物:决策树里我尝试使用花萼长度(Sepal.Length)和花萼宽度(Sepal.Width)这两个变量来预测鸢尾花的种类(Species),这里用随机森林试一试。
首先来看下不同数目的树对分类的影响,下图的分类边界(Decision Boundary),使用的Node Size为1,特征数Feature Count也为1,
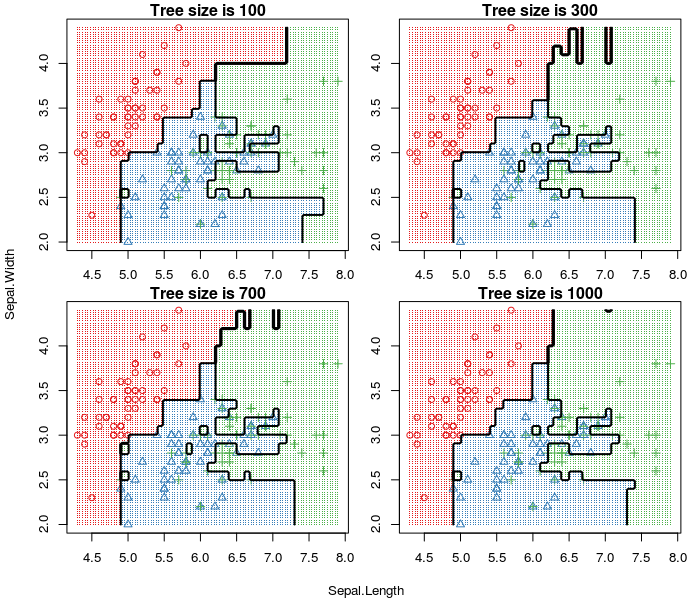
可以看到,与决策树相比,随机森林对过拟合(Overfit)有着很强的抗性,且随着树的数目增多过拟合越来越少。但是,另一方面也要看到尽管对过拟合很强的抗性,还是可以看到过拟合的影子,即便我们已经用了1000棵树。所以,还是要为随机森林选择一个合适的Node Size,
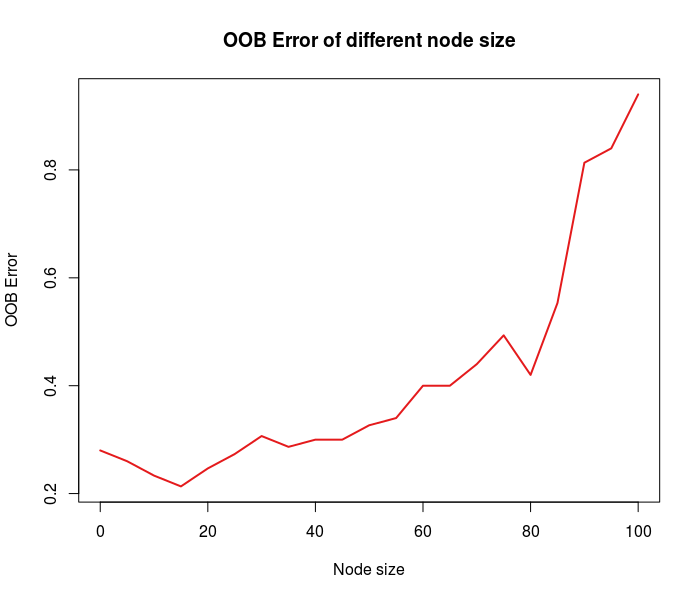
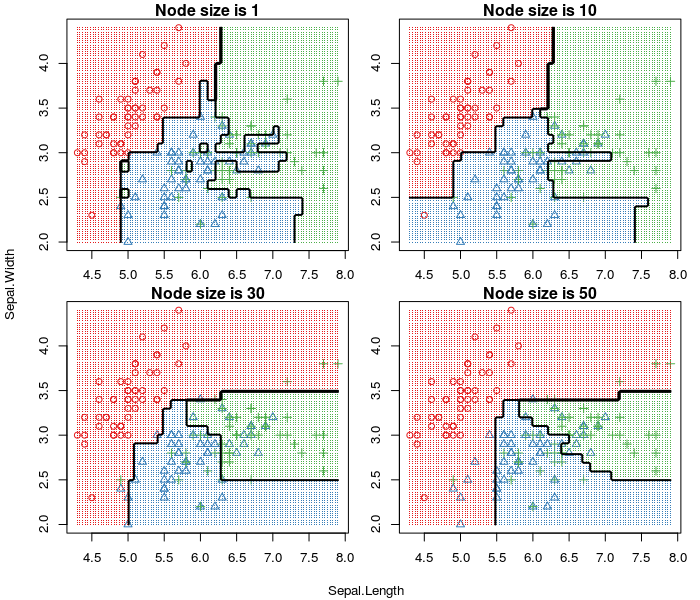
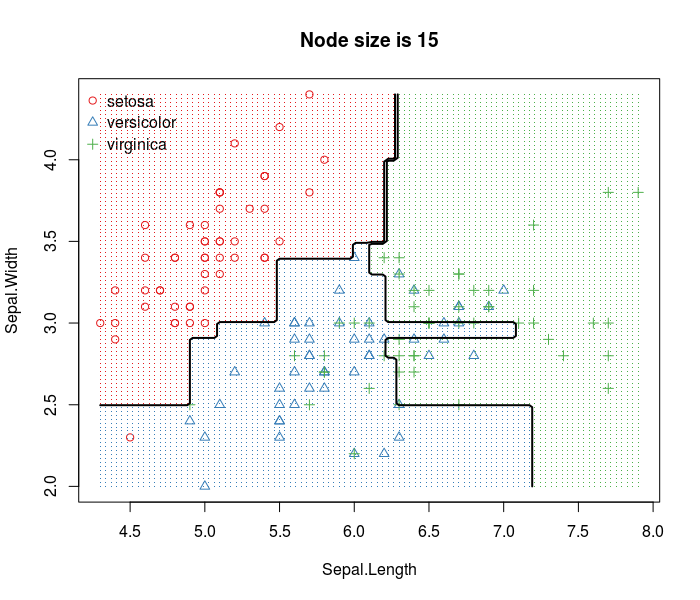
从上面的第一张图,可以看到Node Size从0~100增加时,OOB Error先降后增,且在Node Size为15时达到最低。从第二张图可以看到随机森林分类边界的变化过程,先是轻微的过拟合继而最合适的边界最后严重的欠拟合。第三张图是最合适的分类边界,尽管和决策树一样,预测的错误率都为0.2左右,但是和决策树的分类边界相比,随机森林的边界更平滑。
2、北京二手房
为了和决策树作对比,我也用随机森林来预测下房价(price),也是使用区域(area)、是否学区(school)、是否有地铁(subway)、总价(num)这四个变量,使用的参数为树的数目TS=100,特征数Feature Count=4,节点数目Node Size=5,得到的结果如下,
$r2
[1] 0.7014904
$importance
area 0.48257784
num 0.37338239
school 0.08469551
subway 0.04547572
袋外决策系数R2为0.7,使用模型预测所有房屋价格的决策系数为0.74,比决策树的0.7高了4个百分点,大家不要小看了这4个百分点,在机器学习中哪怕1个百分点都要付出很大的努力。况且,我在这里并没有使用交叉验证获取最佳的参数,只是凭经验选取。另外模型还给出了预测房价各个变量的重要性,可以看到决定房价最重要的就是房子所在的区。
接下来是个分类问题,使用小区(region)、户型(zone)、面积(meters)、朝向(direction)、区域(con)、楼层(floor)、房龄(year)、学区(school)、地铁(subway)、税(tax)、总价(num)、单价(price)来预测区(area)。随机从29790中抽取了10000条数据构造100颗树的随机森林,构建一个100棵树的森林,OOB Error和变量重要性如下,
$oob_error
[1] 0.1241
$importance
con 0.5454
price 0.3717
school 0.1132
year 0.0556
subway 0.0490
region 0.0168
direction 0.0163
meters 0.0043
num 0.0040
zone 0.0026
floor 0.0007
tax 0.0007
OOB Error约为0.12,使用得到的随机森林模型预测29790条房源的区域,误差约为0.08,两者还是比较接近的。不出所料,片区(con)的重要性最高,另外房价(price)、是否学区(school)对房子区域的重要性也决非浪得虚名。
上文提到,随机森林可以作为降维的工具,我从中选择前6个重要的变量重新构建一个随机森林,OOB Error和变量重要性如下,
$oob_error
[1] 0.11
$importance
con 0.5638
price 0.3812
school 0.1140
year 0.0831
subway 0.0490
region 0.0254
可以看到,使用6个变量的OOB Error与使用全部12个变量的OOB Error不相上下。
下面看看有没有潜在的离群点,下图是每套房子的Dissimilarity,
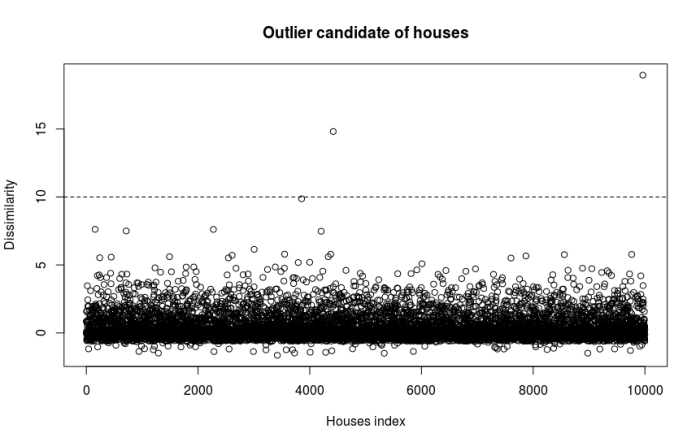
有两套房子的Dissimilarity>10,看看是什么房子,
region zone meters direction con floor year school subway tax num price area
福成公寓A 3室1厅 135 南北 燕郊城区二手房 低楼层 2004 无学区 无地铁 非免税 405 30000 燕郊
达观别墅 4室2厅 270 南北 燕郊城区二手房 低楼层 2009 无学区 无地铁 非免税 1600 59260 燕郊
初步看来,这两套房子的总价(num)和价格(price)有点高,是不是这一点让它们鹤立鸡群呢?
四、总结
本文简单介绍了随机森林的特点及算法,并简单分析了iris和北京二手房两个数据集。本文只是抛砖引玉,其实随机森林的还有一些其他的特性,大家可以多多去发掘。
参考资料: